Лекция 3. Доверительный интервал

Оценка случайной погрешности

Дисперсии V(x) и стандартные отклонения S(x) сами по себе не позволяют проводить вероятностную оценку случайной погрешности. Например, если истинное значение определяемой концентрации= 10 мкг/мл, а стандартное отклонение - = 1 мкг/мл еще не значит, что среди результатов измерений не будет значений 8 мкг/мл, 12 мкг/мл и т.д.

Возникает задача вероятностной оценки погрешности. Возможны три формулировки этой задачи:

1) Известно истинное значение и интервал. Нужно найти вероятность того, что измеренное экспериментально значение попадет в этот интервал.

2) Известно истинное значение и задана вероятность. Нужно найти интервал, в который измеренное значение попадает с этой вероятностью

3) Известно экспериментально измеренное значение и задана вероятность, нужно оценить интервал, в котором находится истинное значение с этой вероятностью.

Задача третьего типа имеет наибольшую практическую значимость, т.к. обычно истинное значение неизвестно, а экспериментратор располагает только измеренными значениями определяемой величины.

Чтобы решить эти задачи, необходима дополнительная информация, а именно: общий вид функции распределения. Например, даже если истинные значения и вероятности (вероятность - площать заштрихованной области на рисунке) совпадают, для разных распределений интервал будет разным:

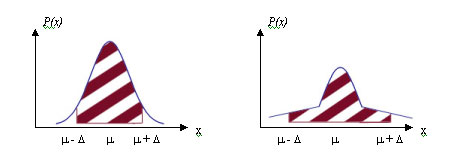
Для результатов химического анализа постулируется нормальное распределение.

Доверительный интервал

, где t(p,f) - коэффициент Стьюдента при заданной доверительной вероятности p (обыно принимается значение 95%) и числе степеней свободы f.

тоже распределены по нормальному закону:

т.о.

Величина - это доверительный интервал, который используется в аналитической химии для оценки воспроизводимости.

лекции читает А.В.Гармаш, химический факультет МГУ