Лекция 15. Погрешность градуировки

В предыдущей лекции были рассмотрены основы построения градуировочной модели. Было отмечено, что измеряемый сигнал содержит погрешность, следовательно, параметры градуировочной модели, а также результаты анализа, полученные с использованием этой модели, также будут содержать погрешность.

Для оценки погрешности в регрессионном анализе вводится понятие дисперсии адекватности (или остаточной дисперсии). Это дисперсия относительно регрессионной модели:

,

где y - экспериментальное значение аналитического сигнала, Y - рассчитаное по уравнению градуировки значение аналитического сигнала, n - число измерений, k - число параметров модели (для линейной градуировки k=2)

Нетрудно заметить, что при построении градуировки методом МНК дисперсия адекватности будет минимальной.

Остаточная дисперсия позволяет оценить адекватность градуировочной модели. Для этого необходимо сравнить дисперсию адекватности и дисперсию воспроизводимости (дисперсию аналитического сигнала для одного образца при серии параллельных измерений) по критерию Фишера:

Возможны три случая:
1) - говорит о том, что выбранная модель плохая. Нужно больше параметров.
2) - означает, что модель "слишком хорошая", перепараметризация. Нужно уменьшить число параметров, т.к. модель описывает еще и погрешность.
3) Различие незначимо - хорошая модель. Если существует несколько хороших моделей, выбирают самую простую. При этом можно усреднить дисперсию адекватности и дисперсию воспроизводимости (с учетом числа степеней свободы) и получить общую дисперсию S²(y), которая будет служить оценкой случайной погрешности модели.

Далее необходимо оценить погрешность коэффициентов модели. Поскольку они расчитываются линейным преобразованием, то они подчиняются нормальному закону распределения. Для расчета соответствующей дисперсии необходимо воспользоваться законом распространения погрешности:

если f = f(x₁, x₂ ... x_n), то - при условии, что аргументы x_i не коррелируют между собой.

В данном случае это условие выполняется (это одна из предпосылок МНК), поэтому, применив закон распространения погрешности к формулам для коэффициентов линейной модели a и b, получим следующие выражения:

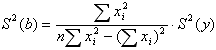
Далее необходимо проверить, значимы ли коэффициенты a и b - т.е. проверить по критерию Стьюдента, значимо ли отличие коэффициентов от нуля.

Если коэффицент b незначимо отличается от нуля, то необходимо его отбросить, перейти к модели y = ax и заново пересчитать уравнение градуировки, дисперсию адекватности и т.д.

Если коэффицент a незначимо отличается от нуля, то это фактически говорит о том, что аналитический сигнал не связан с концентрацией, либо погрешность измерения настолько велика, что на ее фоне невозможно выделить взаимосвязь определяемого содержания и аналитического сигнала. Градуировку в данном случае построить нельзя. Нужно или увеличить число измерений и повторить расчеты, или выбрать другой метод.

Но, как правило, коэффициенты a и b не интересуют аналитика сами по себе. Необходимо расчитать погрешность определения с использованием данной градуировки. При этом возникают два типа задач:

Прямая регрессионная задача. Дано значение x, необходимо оценить соответствующее значение Y и погрешность Y.

Вычисления проводятся по следующей формуле:

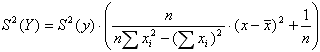
где 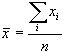(средняя абсцисса всех точек градуировки)

Необходимо отметить следующий факт: S²(Y) - разная, а S²(y) предполагали одинаковой. Особенно велика погрешность за пределами градуировочного графика, т.е. нужно по возможности так выбирать образцы сравнения, чтобы градуировочный график покрывал весь диапазон определяемых содержаний.

Обратная регрессионная задача. Наиболее практически значимый тип задач - по измеренному значению y рассчитать соответствующее значение X и оценить его погрешность:

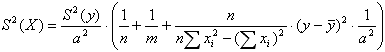
где m - число параллельных измерений,

В приведенной формуле первое слагаемое учитывает погрешность a, второе - вклад погрешности параллельных измерений y, третье - погрешность b.

лекции читает А.В.Гармаш, химический факультет МГУ