Лекция 11. Применение дисперсионного анализа в аналитической химии

Перечислим наиболее распространенные задачи аналитической химии, которые решаются с помощью дисперсионного анализа:

1. Сравнение воспроизводимости результатов или методик.

Эта задача сводится к проверке гипотезы №2 (см. предыдущую лекцию). Например, если стандартные отклонения двух методик различаются, это не всегда означает, что одна методика лучше другой - чтобы утверждать это, необходимо сравнить стандартные отклонения (или дисперсии) с помощью критерия Фишера.

2. Сравнение нескольких средних

Этот тип задач часто возникает при проведении межлабораторных экспериментов, когда один образец анализируется в нескольких лабораториях, а затем полученные результаты анализируются и обобщаются.

Итак, есть m выборок, для каждой рассчитаны дисперсия и среднее . Для удобства будем полагать, что число значений в каждой выборке равно n - это условие не обязательно, но упрощает вычисления.

Сперва нужно убедиться, что дисперсии однородны с помощью критерия Кохрена (или критерия Бартлетта). Если дисперсии неоднородны, то сравнение средних проводить нельзя.

Затем вычисляется дисперсия средних:

, где

И средняя дисперсия:

После чего эти две дисперсии сравниваются между собой по критерию Фишера (среднюю дисперсию при этом нужно поделить на n):

, число степеней свободны дисперсии средних равно m-1, число степеней свободы средней дисперсии - m(n-1)

Если средние различаются незначимо, то различие между средней дисперсией и дисперсией средних также должно быть незначимо.

3. Разложение дисперсии на составляющие

Дисперсия характеризует случайную погрешность и, как правило, складывается из нескольких составляющих. Часто бывает важно оценить вклад каждой составляющей (или фактора) в дисперсию. Например, для оценки погрешности, вносимой на различных этапах аналитической методики.

Как правило, в любой методике можно выделить этап пробоотбора и пробоподготовки, и этап измерения:

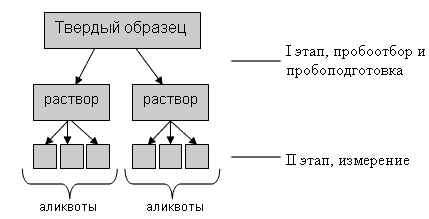
Из образца отбирается несколько проб, которые проходят процедуру пробоподготовки (это может быть вскрытие, экстракция, химическая обработка и т.д.). Для каждой пробы проводится несколько параллельных измерений (например, отбирается несколько аликвот для титрования). В итоге получаем несколько выборок значений, которые обрабатываются по той же схеме, что и при сравнение нескольких средних - вычисляется дисперсия средних и средняя дисперсия.

Средняя дисперсия характеризует второй этап, измерение. А дисперсия средних включает погрешность обоих этапов. Поэтому если дисперсия средних значимо больше средней дисперсии - это означает, что I этап, пробоотбор и пробоподготовка, вносят значимую погрешность в результат анализа и их методика нуждается в усовершенствовании.

лекции читает А.В.Гармаш, химический факультет МГУ