Лекции "Основы хемометрики и химической метрологии"

Лекция 9. Проверка выполнения нормального закона распределения

В предыдущей лекции было показано, что результаты химического анализа, как правило, подчиняются нормальному распределению. Исходя из этого выбираются критерии для проверки статистических гипотез. Однако, если распределение отличается от нормального, то критерии для нормального распределения (такие, как критерий Стьюдента) применять нельзя.

Поэтому вид распределения нужно предварительно проверять. Существуют статистические критерии подчинения нормальному закону распределения.

1) Грубые критерии. Эти критерии определяют, есть ли резко выпадающие данные (грубые ошибки, промахи, выбросы). Эти критерии не рассматривают всей совокупности данных, а только крайние значение. Примером может служить Q-критерий. Тестовая статистика Q-критерия вычисляется по формуле:

где x_? - "подозрительное" значение (вероятный промах) - это максимальное или минимальное значение выборки, x_{ближайшее} - ближайшее к подозрительному значение, x_мин и x_макс - максимальное и минимальное значения выборки (эта формула верна для числа измерений n = 3..7. При n = 8..10 в знаменателе должна стоять разница между подозрительным значением и ближайшем к максимальному (или минимальному)). Значение Q сравнивают с табличным значением, и если табличное значение критерия меньше тестовой статистики, то подозрительный результат является промахом и исключается из дальнейшего рассмотрения. При этом обычно доверительную вероятность берут равной 0.90, а не 0.95. В данном случае это является некоторым "ужесточением" требований: лучше выбросить значение, не являющееся промахом, чем оставить промах в выборке. Как правило, на промах проверяют минимальное и максимальное значение выборки.

Q-критерий работает для выборок, содержащих 3 - 10 значений, при больших объемах выборки он становится нечувствителен к промахам.

2) Критерии, которые определяют, подчиняется ли вся совокупность нормальному распределению. Для применения этих критериев обычно требуется большой набор данных (чем больше, тем лучше, как правило, не меньше 30 единичных измерений).

Один из наиболее простых критериев этого типа - критерий Пирсена. Проверка гипотезы о нормальном распределении случайной величины осуществляется по следующей схеме:

Дана выборка из n значений: x₁, x₂ ... x_{n, причем n > 30}

Значения упорядочиваются по возрастанию, и вся выборка разбивается на m интервалов, m > 5, (обычно берут ), причем в каждый интервал должно попадать не менее 5 значений:

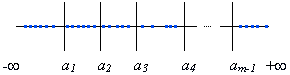
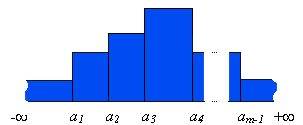
Строится гистограмма, площадь прямоугольника над отрезком должна быть пропорциональна числу точек, попавшему в отрезок (N_i):

Нужно выяснить, случайно ли отличие от нормального распределения, другими словами, случайно ли различие между экспериментальной кривой и теоретической кривой. Теоретическая кривая строится по формуле:

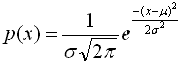
причем в качестве и берутся соответственно значения среднего и стандартного отклонения S, вычисленные для тестируемой выборки.

Нужно охарактеризовать различие между площадью экспериментальной гистограммы и площадью под теоретической кривой. Интеграл от функции Гаусса не выражается в элементарных функциях, но существуют таблицы интегралов для функции:

Для того, чтобы теоретическую кривую привести к такому виду, нужно произвести замену переменных:

Аналогично преобразовываются координаты отрезков:

Строится таблица:

отрезок	исходные границы		преобразованные границы		интеграл от функции гаусса
	левая	правая	левая	правая	(вычисляется по таблице)
1		a1		b1	I1
2 . . .	a1	a2	b1	b2	I2
m	am-1		bm-1		Im

Поскольку интеграл I_i равен доле точек (сумма этих интегралов должна быть равна 1), то его нужно умножить на число точек:

Вычисляется тестовая статистика:

Тестовая статистика сравнивается с табличным значением . Если тестовая статистика больше табличного значения, гипотеза о нормальном распределении отбрасывается, если меньше - данные подчиняются нормальному распределению.

лекции читает А.В.Гармаш, химический факультет МГУ

<< Предыдущая лекция Следующая лекция >>

Содержание

4 февраля 2006

Ваше имя:
Текст сообщения: