Лекции "Основы хемометрики и химической метрологии"

Лекция 4. Оценка систематической погрешности

Способы количественной оценки правильности (систематической погрешности)

Систематическая погрешность (см. лекцию 2).

Таким образом, чтобы найти , нужно сопоставить с

Здесь возникают две проблемы:
1) с чем сравнивать? (где взять ?)
2) как сравнивать?

1) сравнивают с арбитражным значением , полагают, что ~

Требования:
- не содержит погрешности
- случайная погрешность меньше случайной погрешности результатов

Способы получения :
- независимый анализ (более точной методикой, а лучше другим методом)
- введено-найдено (по существу сравнение с гравиметрией)
- анализ стандартных образцов - самый надежный способ

2) Действительное значение измеряемой величины - это (систематическая и случайная погрешности пренебрежимо малы) - постулируется, как . Обозначается a(x) = const
Но у нас нет , есть , которое содержит случайную погрешность. Чем обусловлена разница между и a - случайной или систематической погрешностью? Случайную погрешность на фоне систематической обнаружить легко. Систематическую на фоне случайной - сложно. Поэтому если неравенство можно объяснить случайной погрешностью, считается, что систематической погрешности нет ("презумпция правильности").

Выявление систематической погрешности

Ссылки по теме:
Он-лайн программа для расчета доверительного интервала
Таблица значений критерия Стьюдента

1. Если есть значение a:

сравниваем и a(x) , т.е. попадает ли a в доверительный интервал.
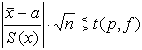, где t - табличное значение критерия Стьюдента при заданной доверительной вероятности p (обычно полагается равной 0.95) и числе степеней свободы f = n-1