Лекции "Основы хемометрики и химической метрологии"
Лекция 12. Корреляционный анализ
Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными величинами.
Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию - о взаимосвязи этих параметров.
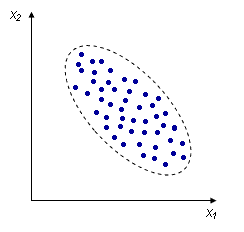
Например, измеряем рос и вес человека, каждое измерение представлено точкой в двумерном пространстве:
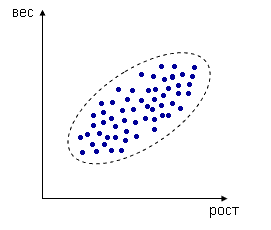
Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость - корреляция.
В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:
|
Отрицательная корреляция:
|
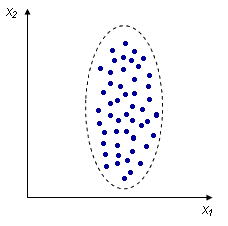
Отсутствие корреляции:
|
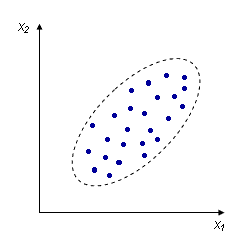
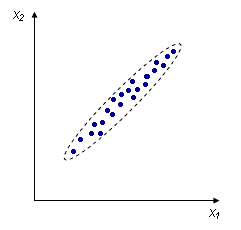
Корреляцию необходимо охарактеризовать численно, чтобы, например, различать такие случаи:
|
|
|
Для этого вводится коэффициент корреляции. Он рассчитывается следующим образом:
Есть массив из n точек {x1,i, x2,i}
Рассчитываются средние значения для каждого параметра: ![]()
И коэффициент корреляции: 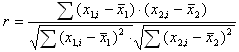
r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x1 и x2: r равен 1 (или -1), если связь линейна.
Коэффициент корреляции является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:
1. Коэффициент корреляции значимо отличается от нуля (т.е. корреляция есть):
Тестовая статистика вычисляется по формуле:
![]()
и сравнивается с табличным значением коэффициента Стьюдента t(p = 0.95, f = ![]() ) = 1.96
) = 1.96
Если тестовая статистика больше табличного значения, то коэффициент значимо отличается от нуля. По формуле видно, что чем больше измерений n, тем лучше (больше тестовая статистика, вероятнее, что коэффициент значимо отличается от нуля)
2. Отличие между двумя коэффициентами корреляции значимо:
Тестовая статистика:
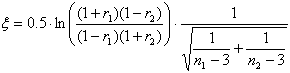
Также сравнивается с табличным значением t(p,![]() )
)
Методами корреляционного анализа решаются следующие задачи:
1) Взаимосвязь. Есть ли взаимосвязь между параметрами?
2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.
3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.
лекции читает А.В.Гармаш, химический факультет МГУ
<< Предыдущая лекция Следующая лекция >>
16 февраля 2006
Если у Вас есть комментарии или вопросы по этой лекции, Вы можете оставить свое сообщение:
всего сообщений: 1
сообщение оставлено Сергиенко Марина, 20 марта 2007 21:32:23)
Объясните, если не трудно, зачем узнавать, значимо ли коэффициент корреляции отличается от нуля, если в тестовой статистике используется само значение коэффициента корреляции, то есть мы его уже знаем? И второй вопрос, откуда берется утверждение, что "чем больше измерений n, тем лучше (больше тестовая статистика, вероятнее, что коэффициент значимо отличается от нуля) "? Мне кажется, что чем больше количество наблюдений, тем точнее можно определить коэффициент корреляции, а больше или меньше нуля этот коэффициент, не имеет значения. Большое спасибо за будущий ответ
Использование материалов сайта разрешается только при наличии текстовой гиперссылки на этот сайт.
Статистика в аналитической химии copyright © 2005-2006