Лекция 8. Нормальное распределение

Любая случайная величина имеет функцию распределения - зависимость плотности вероятности от значения случайной величины. Для нормального распределения (распределения Гаусса) функция распределения имеет следующий вид:

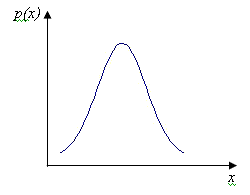
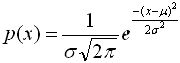
- матожидание (генеральное среднее)
- стандартное отклонение

Для проведения статистических расчетов часто необходимо располагать информацией о виде функции распределения.

Центральная предельная теорема Чебышева: Если случайная величина подвержена воздействию бесконечного числа бесконечно малых случайных факторов, то она имеет нормальное распределение.

Как правило, для аналитических измерений условие теоремы выполняется, поэтому для результатов химического анализа обычно постулируется нормальное распределение.

Нарушения нормального закона распределения:

1) Нарушаются условия теоремы (выделяется более весомая группа факторов). Например: анализ высокочистых веществ - неравномерное распределение примесей.

2) Произвольное объединение нескольких выборок (даже если каждая из них подчинялась распределению Гаусса):

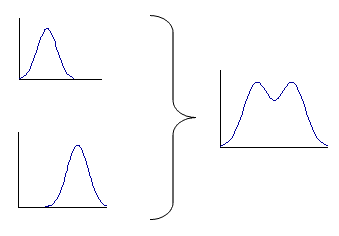
3) Косвенные измерения. Линейная комбинация нормально распределенных случайных величин также будет подчиняться нормальному распределению. А нелинейная комбинация (например, произведение двух величин) не сохранит нормального распределения. Однако, чем меньше погрешность, тем меньше отличие от нормального распределения, поэтому даже для нелинейных преобразований в некоторых случаях можно принять нормальное распределение.

4) Результат измерения является дискретной величиной (например, некоторые радиоактивационные методы анализа, ряд биохимических и рентгеноспектральных методов - так называемые счетные методы). В этом случае результат измерения подчиняется распределению Пуассона. Однако при больших распределение Пуассона переходит в нормальное распределение. (Примечание: формально любой результат измерения является дискретным - потому, что шкала прибора имеет дискретный набор делений, и результат округляется до ближайшего деления. Однако если измеряемый сигнал много больше цены деления, то результат подчиняется нормальному распределению).

Что делать, если результат не подчиняется нормальному распределению?
1) Возможно, нормальное распределение выполняется приблизительно и можно применять критерии для нормального распределения.
2) Если известен закон распределения (например, распределение Пуассона), то можно пользоваться критериями этого распределения. (Например, для сравнения двух нормально распределенных случайных величин используется критерий Стьюдента - см. Лекцию 4. Дисперсия рассчитывается нелинейным преобразованием, и подчиняется -распределению (хи-квадрат распределение или распределение Фишера). Для сравнения двух дисперсий используется критерий Фишера.
3) Если распределение неизвестно, то на этот случай существуют непараметрические критерии. Например, сравнение двух средних на основе расчета числа возможных перестановок внутри объединенной выборки.

Как проверить, выполняется ли нормальный закон распределения, читайте в следующих лекциях.

лекции читает А.В.Гармаш, химический факультет МГУ