Лекция 10. Основы дисперсионного анализа
Дисперсионный анализ включает в себя проверку гипотез, связанных с оценкой выборочной дисперсии. Можно выделить три основных вида гипотез:
1. 
(значимо ли различие между двумя дисперсиями?)
2. 
(одна дисперсия значимо больше другой?)
3. 
(значимо ли различие между несколькими дисперсиями?)
Дисперсия вычисляется из случайных величин, и поэтому сама также является случайной величиной. Напомним, что дисперсии, в отличие от средних, подчиняются распределению 
Ссылки по теме:
- Он-лайн программа для сравнения двух дисперсий
- Таблица значений критерия Фишера
- Лекция 4. Оценка систематической погрешности. Сравнение дисперсий
Первые две гипотезы дисперсионного анализа проверяются с помощью критерия Фишера. Причем 1-я гипотеза - с помощью двустороннего критерия, а вторая - с помощью одностороннего. Строго говоря, эти критерии не равны, но в общем случае разницей можно пренебречь. Проверка производится по следующей формуле:
С 3-й гипотезой (сравнение нескольких дисперсий или проверка однородности дисперсий) дело обстоит сложнее. Попарно сравнивать дисперсии некорректно (например, какой вывод нужно сделать, если из трех дисперсий дисперсии 1, 2 и 1, 3 различаются незначимо, а дисперсии 2, 3 - значимо?). В дисперсионном анализе для сравнения нескольких дисперсий существует два критерия:
1. Критерий Бартлетта
Критерий Бартлетта включает в себя довольно сложные вычисления (подробнее см. книгу К. Дерффель "Статистика в аналитической химии). Тестовая статистика сравнивается с процентной точкой распределения.
Плюсы: нет требования равенства числа степеней свободы дисперсий, критерий выявляет отклонения как в наибольшую, так и в наименьшую стороны
Минусы: сложность вычислений, число степеней свободы любой дисперсии должно быть больше трех, критерий очень чувствителен к нарушению нормального закона распределения исходных данных.
2. Критерий Кохрена
Проверка однородности дисперсий включает вычисление доли максимальной дисперсии среди всех дисперсий:
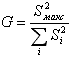
которая затем сравнивается с критическим значением G(p,m,f), где f - число степеней свободы каждой дисперсии (должно быть одинаковым у всех дисперсий), m - число дисперсий, p - доверительная вероятность.
Плюсы: простота вычислений
Минусы: ограничение на число степеней свободы дисперсий, критерий выявляет отклонения только в большую сторону.
Сравнивая плюсы и минусы критериев Бартлетта и Кохрена, можно увидеть, что они являются взаимодополняющими и должны использоваться совместно.
О применении дисперсионного анализа в аналитической химии читайте в следующей лекции.
лекции читает А.В.Гармаш, химический факультет МГУ
